The second characteristic that inhibits CCD cameras is their high level of random noise. A typical CCD camera used with an 8-bit digitizer yielding 256 counts, has 2 to 6 counts of random noise in the baseline. The noise is typically Gaussian, and goes both positive and negative about a mean or average baseline level. When normal baseline subtraction occurs, the negative noise components are truncated, leaving only the positive components. These lost negative noise components can distort measurements that rely on low intensity background.
Situations exist in which the baseline offset and lost negative noise components are very significant. For example, in image processing, when attempting to distinguish data with a very low contrast between objects, the contrast is compromised by the loss of the negative noise. Secondly the measurement of laser beam widths requires analysis of very low intensity signals far out into the wings of the beam. The intensity is low, but the area is large, and so even small distortions can create significant errors in measuring beam width.
The effect of baseline error is particularly significant on the measurement of a laser beam width. This measurement is very important because it gives the size of the beam at the measurement point, it is used in laser divergence measurement, and it is critical for realistic measurement of M2, the ultimate criterion for the quality of a laser beam. One measurement of laser beam width, called second moment, or D4, which is the ISO definition of a true laser beam width, is especially sensitive to noise in the baseline. The D4 measurement method integrates all signals far out into the wings of the beam, and gives particular weight to the noise and signal in the wings. It is impossible to make this measurement without the negative noise components, and without other special algorithms to limit the effect of noise in the wings.
To determine the effect of special measurement algorithms generated by Spiricon, a simulated beam width calculation was performed. A mathematically generated Gaussian beam was computer generated so it would be a defined known width. (It is impossible to tell the accuracy of measuring beam width if you don't know the beam width to start with.) Random noise with a Gaussian distribution was then added to the mathematically generated Gaussian beam. Measurements were then made using Spiricon algorithms to determine the accuracy of measuring beam width with typical noise included.

Figure 1. Theoretical beam width error vs. the number of pixels for both a D4 and a knife-edge measurement without an aperture.
Figure 1 illustrates the calculated beam width error vs. beam size without all components of Spiricon's Ultracal algorithms. Note that in a 512X512 camera array, a beam width only as small as 64X64 is calculated at 60% error using the D4 method. This theoretically confirms previous reports of the errors generated by the presence of noise in D4 measurements. Also shown in Figure 1, is the beam width error calculated using the conventional knife-edge DKE method, which generates only 3% error at 64X64 beam size. Thus, while D4 is the theoretically correct way to measure a beam width, the practical problems of noise in the camera, have precluded its use up to this point.
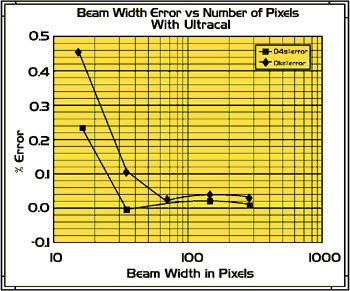
Figure 2. Theoretical beam width error for D4 and knife-edge measurements using an aperture of two times the width of the beam.
Using the knowledge gained from the simulations of Figure 1, Spiricon engineers have developed a new calculation algorithm, Ultracal, that enables accurate D4 measurement in the presence of camera noise. Under the same conditions of the simulations of Figure 1, the simulated measurement accuracy of the new algorithms is shown in Figure 2. A D4 calculation is now made with only 0.25% error (vs. 60%) down to a 16X16 beam width, even beating the knife-edge DKEmethod error of 0.5%. These are astoundingly accurate results. In fact, these are the first reported results that an accurate D4 measurement can be made with commercial grade CCD cameras.
Many factors can contribute to the accuracy of a laser beam width measurement with CCD cameras. These factors are listed independently here, but they all interact with each other. These factors include:
The number of CCD pixels included in the beam width, i.e., what is the size of the beam in camera pixels? The number of pixels in the digitized camera field, i.e., a small beam and a large digitized field can compromise measurement accuracy due to noise in the large field. The beam width measurement method. This includes the ISO standard D4, the alternate Knife-Edge (KE) method, and the more traditional methods of % of Energy or % of Peak. The measurement can be made with or without an aperture around the beam. (An aperture limits noise outside the area of interest in making the beam measurement.) The intensity of the beam; that is, a beam near saturation has a larger signal-to-noise ratio than a beam with the peak at 10% of saturation. Finally, negative numbers in the noise floor can significantly affect the measurement accuracy, especially of the D4 measurement. Whether the digitizer retains negative numbers, or truncates negative numbers, can have a strong effect on the measurement accuracy.
These factors have been investigated by measurements on a real laser beam. While the following charts show beam width error as the vertical column, they really measure "beam width non-consistency." Since this is a beam of unknown width, except as measured by the CCD camera, the true beam width is not known. However, for the sake of simplicity, the beam width measured under the assumed most accurate and consistent conditions, has been taken as a reference. All other beam widths are measured relative to that reference. It was also deemed that a log/log plot was the most interesting for viewing of the accuracy data . Some examples of these measurement combinations are shown in the following graphs.
It has been shown in the past that most beams, including Gaussian beams, have significant energy in the wings, up to 2 times the 1/e2 beam width. Any fixture that clips the beam smaller than twice the beam width, can cause diffraction in the beam. If a measurement aperture is less than twice the beam width, then clipping of signal in the wings occurs, and a reported beam width smaller than the real beam width is given. At about 2 times the beam width, the optimum measurement is made, wherein no significant clipping occurs, yet the maximum amount of noise in the wings of the beam is eliminated. Spiricon engineers have created an algorithm that automatically sets an aperture at 2 times the measured beam width.

Figure 3. Comparison of a D4 beam width measurement with and without an aperture vs. the number of pixels in the beam.
Figure 3 shows a measurement using the second moment, or D4 measurement method, with and without an aperture vs. the number of pixels in the beam. This beam was of high intensity, being about 230 digital counts out of 255 possible counts. The number of pixels in the beam was reduced, but not by focusing the beam. Instead, the beam analyzer was made to sample every second, fourth, and eighth pixel, etc. in every second, fourth, and eighth row, so that the beam was sampled consecutively by fewer and fewer pixels. Since the original beam width was known with a high resolution sampling, it was possible to tell how much error was introduced by having only a few pixels in the beam. This is analogous to having a small focused spot of only a few pixels width, but not exactly the same. A focused beam measurement would be the subject of a future study.
Figure 3 shows that there is about a factor of 10 difference between measuring the beam width with and without an aperture. The measurement with an aperture gave about 0.2% error down to 11 pixels. The error is as low as 3%, down to only 2.8 pixels in the beam. Without the aperture the beam had to be at least 11 pixels to obtain the same accuracy. However, a 5% error is obtained with only 5.6 pixels in the beam. It should be emphasized that this measurement was made with all other parameters set at the optimum. That is, the negative noise components of the noise are being used, the field of the camera is 256X240, which is only slightly larger than the 2X beam width needed, and the precise baseline calibration was performed immediately before these measurements.

Figure 4. Comparison of the D4 vs. a knife-edge measurement, using apertures in both measurements, vs. the number of pixels in the beam.
Figure 4 shows a comparison of the knife-edge method of measurement of the beam width vs. the D4. When an aperture is used, the D4 measurement is slightly more accurate than the knife-edge measurement. It should be pointed out that all of these measurements are less than 1% error. Thus until the pixels become less than 8, the measurements are within experimental electro-optic accuracy, and both measurements would be totally acceptable.

Figure 5. Comparison of the accuracy of D4 vs. knife-edge measurement without an aperture in the beam.
Figure 5 shows the measurement accuracy of knife-edge vs. D4 without an aperture. In this case, the knife-edge is considerably more accurate than the D4 measurement. This is expected because D4 is intrinsically susceptible to noise out in the wings of the beam. The knife-edge method averages that noise, and is not nearly as susceptible to noise beyond twice the beam width. The knife-edge measurement is still less than 1% error, which is totally acceptable down to 10 pixels, whereas the D4 measurement is up in the 3-4% error range, which is not nearly as good as with an aperture. This graph clearly shows, as compared with the previous graph, the value of an aperture in making D4 measurements.

Figure 6. The effect of a D4 measurement using an aperture, but comparing with and without retaining negative noise components.
Figure 6 shows the effect of keeping negative numbers in the baseline. Without keeping negative numbers, only positive noise components are kept. This is the way most digitizers work. With only positive noise components, the measurement would attribute all of the positive noise components to be partially signal, and thus measure a beam larger than in actuality. In this figure we see that with an aperture, the D4 measurement is approximately 5 times better with the negative noise components considered, than without.

Figure 7. Comparison of D4 with and without negative numbers vs. number of pixels in the beam without an aperture to limit noise in the beam.
Figure 7 shows negative noise component effect much more dramatically. In this case we have removed the aperture, and measured the beam width with and without negative numbers in the baseline. In this case, again using D4 measurements, both are worse without the aperture. But without the negative noise, the measurement error becomes greater than 10%, which is totally unacceptable. This dramatically illustrates the effect of noise in the wings when negative noise components are not considered.

Figure 8. Measurement of beam width accuracy using D4 with and without an aperture vs. the peak intensity level in the beam. (Negative noise components are retained in both measurements.)
Figure 8 switches to measuring beam width accuracy vs. intensity, rather than beam size. The comparison is with and without an aperture. Here a large area beam covering 90 pixels and a 256X240 field is measured at full intensity, roughly 230 counts. The beam intensity is then reduced with neutral density filters, and the width measured. The D4 method with an aperture is able to measure with less than 0.5% error down to 43 counts, and less than 3% error all the way down to 15 counts in the beam peak. 15 counts in the beam peak is less than 6% of saturation. However, without an aperture, the measurement is in the 3-6% error range at all intensities, which is unacceptable. If the field was larger or the beam smaller, the differences between these two measurements are even more dramatic.

Figure 9. D4 measurement using an aperture, but with and without negative noise components vs. the intensity of the peak signal in the beam.
Figure 9 illustrates the effect of retaining the negative numbers in the noise when measuring low intensity signals. In this case, an aperture is used to minimize noise contributions for both measurements. With negative noise components removed, the beam width error measurement increases rapidly and dramatically as the intensity is reduced. However, with negative noise components retained, a measurement error of less than 0.6% is achieved with only a 43 count signal peak. This is only 17% of saturation. A 3% measurement is obtainable at 15 counts, or 6% of the peak signal intensity. As shown in the next section using other algorythms, a 6% measurement is possible with a signal as small as 1 digital count, or only 0.4% of saturation.
These measurements illustrate the effects of various parameters of measuring beam widths. They show that it is possible to accurately measure a beam as small as just a few camera pixels in width, as long as other parameters are kept at their optimum. They also show that it is possible to measure a beam of fairly low peak intensity, using proper beam measurement algorithms. The parameters that should be under control of the operator, are first, the number of pixels in the digitized camera field. Here the operator would want to minimize the digitized camera area and number of pixels to only incorporate what is needed to include the beam. This minimizes the amount of noise being contributed beyond the wings of the beam. Secondly, both D4 and knife-edge give relatively accurate measurements of the beam. The D4 is preferred if the beam is not Gaussian. The knife-edge uses a correction factor, which is optimized for most beams, but not for all. Third, an aperture placed around the beam increases the beam width measurement accuracy by nearly a factor of 10 in most cases. Retaining negative numbers in the noise floor can be extremely important. For high intensity beams that are large enough to fill the camera, the negative numbers are not as significant. However, if the peak beam intensity falls much less than saturation, or if a small beam of only a few pixels in a large field is measured, then retaining the negative numbers give more than a factor of 10 improvement in accuracy.
Retaining the negative numbers in the camera baseline field enables signal processing that would not otherwise be possible. One example of this processing is frame summing. If the negative noise components are eliminated, as is the case with most digitizers, frame summing would cause all of the positive noise components to continually add, and ultimately produce a net positive baseline offset. This would make frame summing essentially a worthless exercise. However, with negative numbers retained, the negative noise components subtract from the positive noise components on a frame-by-frame basis, and keep the mean noise distribution near zero. The size of the noise, however, adds roughly as the square root of the number of frames summed. However, the signal grows roughly as the number of frames. Thus the signal-to-noise ratio improves roughly as the square root of the number of frames summed. Summing is used in the following example to show the dramatic effect that can be obtained with the retention of the negative numbers.

Figure 10. HeNe near Gaussian beam measured and displayed at nearly full intensity.
The utility of frame summing signal processing is shown with a low intensity beam. A laser beam signal was attenuated until it was buried in the noise so that the peak was approximately 1 digital count. The noise was approximately 3 digital counts. For reference, Figure 10 shows a 3D picture of the beam at its full intensity.

Figure 11. 3D display of noise field with summing of 256 frames.
With attenuation, the beam was reduced to the point where it was not visible in the display. To show the accuracy of the baseline calibration, the beam was first blocked completely, and the baseline was summed over 256 frames. Figure 11 shows a 3D picture of this noise field. Notice the large amount of noise. The negative noise components are shown in gray, going below the colored positive noise components.

Figure 12. Histogram of the noise of Figure 11. (Histogram shows the number of pixel counts at each intensity level.
The LBA-300PC produces a histogram of all signals. Figure 12 shows the histogram of the 256 sum noise baseline from Figure 11. In the histogram the noise is centered very close to zero, with roughly a Gaussian distribution plus or minus about zero. A close inspection of Figure 12 shows that the noise is centered slightly below zero. This is because the camera which had only been turned on for about 15 minutes was still warming up and the baseline was drifting. Thus, even though the measurement was made immediately after an Ultracal, during that period the baseline drifted just slightly, giving this small baseline offset. Spiricon's "Mantra" is "Ultracal early, and Ultracal often."

Figure 13. 3D image of laser beam of about 1 count intensity after 256 frames of summing.
Another Ultracal was performed, then immediately afterwards the 1 count beam was unblocked, and a sum of 256 frames of that beam was made. This beam profile is shown in Figure 13. The laser beam rises up out of the noise, even though the noise level around it is still very high. The noise level on the beam itself is also very high. Nevertheless, the knife-edge measurement was able to measure the beam width immersed in all this noise, as shown at the top of the picture. This is a beam width error, from the unattenuated beam, of less than 5%. D4 measurement gave about 7% error which is also very good.

Figure 14. The beam of Figure 13 displayed with a 4X4 pixel averaging to create a single pixel.
One feature of the LBA-300PC is to average adjacent pixels for display purposes only. Thus with a 256X240 camera field, you can average 4X4 pixels into a single pixel, and display it as 64X60. This is shown in Figure 14. The beam of Figure 13 is now clearly discernible above the noise. One reason the knife-edge measurement algorithm can measure the beam accurately is that it uses an averaging technique to measure beam width. This figure illustrates why it is able to measure a beam in the midst of such large noise.

Figure 15. Convolution of 7X7 pixels of the beam of Figure 13.
The LBA-300PC also has other signal processing algorithms that can be used to improve the measurement of beams and other objects. One of these is convolution, which can be used to suppress noise. Figure 15 shows the beam of Figure 13, with a convolution of 7X7 pixels. This clears up the noise even better than the pixel averaging of Figure 14. However, the convolution causes a slightly reduced beam width measurement. It is now measured at a 7% error vs. a 5% error from Figure 13. All in all, a 7% error in beam width measurement is not bad for a laser beam that was only 1 count high in 3 counts of noise.
e have shown that there are many factors that contribute to the accuracy of laser beam width measurements. The primary things that should be in control of the operator are the accuracy of the baseline (keeping it near zero), maintaining the negative noise components in the baseline so that they can offset positive noise components, using apertures to limit the area of the measurement so that additional noise does not distort the measurement. Finally, the measurement algorithms such as the knife-edge, or the D4, or other methods, can be very significant in assessing the width of the beam.
Keeping the negative noise components in the camera field enables other signal processing, which could be useful for many applications besides laser beam measurements. This enables averaging, summing, convolution, and other signal processing enhancements. We believe that the LBA-300PC frame-grabber and software are a unique contribution to the technical community. It offers features for laser beam profiling, as well as many other applications.
















 Ultra-High Velocity
Ultra-High Velocity